Triangles

by Stan Burech

The Problem

It takes 3 non-parallel lines to make a triangle. If there are more than 3 non-parallel lines, how many triangles do they make?

Illustration

To visualize the problem use between 3 and 7 lines (more than 7 becomes too cumbersome to draw), run the procedure Triangles? :Lines inserting the number of lines you want to see (example: Triangles 7) and try counting them yourself.

TERRAPIN LOGO DOES THE HEAVY LIFTING: Now let Terrapin Logo count the triangles for you by running TriangleCount :Lines.

The Mathematics

This problem comes from a branch of mathematics called combinatorics. Combinatorics uses factorials. There is another procedure in the Terrapin Logo library employing factorials.

Here is the reasoning for solving the number of triangles created by seven non-parallel lines. There are 7 lines, so one line can be one side of the triangle. The second side of the triangle can be from the six remaining lines and the third choice from the remaining five lines. The total number of ways you can choose the sides of the triangle is 7x6x5. but you don’t want to say there are six triangles when there is really only one simply because you can use the same three sides to create the same triangle in six different orders. So, divide out this redundancy and the answer becomes (7x6x5) / 6 = 35. And the general formula for any number of lines, therefore, is C (N,R) = N! / (N - R)! R! where N is the number of lines and R is the number of choices out of the seven lines, or 3 for the making the triangles. For 7 lines:

C(N,R) = 7!/ (7-3)! x 3! = 5040/ 24 x 6 = 5 -1) = 5040/144 = 35.

You now should be able to understand why, if you have a bag of six sticks of six different colors, and you pull out three, you have 20 different color combinations possible: 6 x 5 x 4 / 6. (Demonstrating the failure of most people to understand the basics of combinatorics and other rational behaviors won Daniel Kahneman a Nobel Prize in Economics.)

HAVE FUN WHILE TERRAPIN LOGO DOES THE WORK: Run 51976 non-parallel lines in the procedure TriangleCount :Lines (TriangleCount 51976) and see how fast Terrapin Logo counts the number of triangles. (Answer: 23,400,882,905,400 triangles). Now work out the math for 9 non-parallel lines:

(9!/(9-3)!3! = 362,880/6!3! = 362,880/720x6 = 362,880/ 4320 = 84)

and then check it against the procedure TriangleCount :Lines

HAVING TROUBLE SEEING THE TRIANGLES? Calculate how many triangles there should be with 5 non-parallel lines:

5!/(5-3)! x 3! = 120/(2 x 6) = 120/12 = 10

or just run the procedure TriangleCount 5.

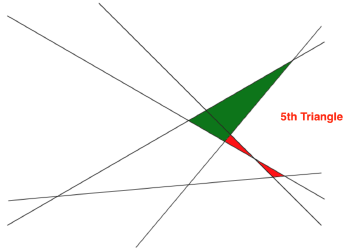
To see the 10 triangles formed from 5 non-parallel lines, run the procedure ColorTriangles5 (5 non-parallel lines were chosen to illustrate how to find the triangles because less than five becomes trite and more than five becomes too messy).

TO TRICOUNT :LINES
	OP :LINES * (:LINES - 1) * (:LINES - 2) / 6
END

TO TRIANGLES? :LINES
(If :Lines > 7 PR [For illustration purposes the number of lines allowed in this procedure is limited to 7.  Try again.] Stop)
	IF :LINES < 1 [HT STOP]
	PU (RUN ITEM :LINES [ 
    ( (SETXY [-300 200]) PD RT 120 FD 700 PU HOME)
    ( (SETXY [-300 -200]) PD RT 60 FD 700 PU HOME) 
    ( (SETXY [300 180]) PD LT 140 FD 550 PU HOME) 
    ( (SETXY [300 -200]) PD LT 45 FD 600 PU HOME) 
    ( (SETXY [300 -100]) PD LT 95 FD 600 PU HOME) 
    ( (SETXY [10 -200]) PD RT 5 FD 450 PU HOME) 
    ( (SETXY [-500 20]) PD RT 85 FD 850 PU HOME)
  ])
	TRIANGLES? :LINES - 1
END

To TriangleCount :lines
  (Pr "with :lines "non-parallel "lines "you "will "find)
  (Pr TriCount :lines "triangles)
end

To ColorTriangles5
  cs
  wait 1000
  Setpc "black
  Triangles? 5
  Pr [According to the analysis there should be 10 triangles with 5 non-parallel lines. Keep count as each of the 10 triangles appears]
  wait 1000
  PR [Here is the first triangle]
  wait 1000
  play "typekey
  pu setxy [130 -40] setpc "red pd fill pu
  wait 6000
  pr [Here is the second triangle]
  wait 1000
  play "typekey
  setxy [75 0] pd setpc "red fill pu
  wait 6000
  pr [Here is the third triangle]
  wait 1000
  play "typekey
  setxy [210 -100] pd setpc "red fill pu
  wait 6000
  pr [Here is the fourth triangle]
  wait 1000
  play "typekey
  setxy [120 0 ] pd setpc "green fill pu
  wait 6000
  pr [Here is the fifth triangle]
  wait 1000
  play "typekey
  setxy [85 0 ] pd setpc "green fill pu
  wait 6000
  pr [Here is the sixth triangle]
  wait 1000
  play "typekey
  setxy [85 -45] pd setpc "green fill pu
  wait 6000
  pr [Here is the seventh triangle]
  wait 1000
  play "typekey
  setxy [85 -105] pd setpc "green fill pu setxy [210 -100] pd fill pu
  wait 6000
  pr [Here is the eighth triangle]
  wait 1000
  play "typekey
  setxy [85 -105] pd setpc "blue fill pu setxy [210 -105] pd fill pu
  wait 6000
  pr [Here is the nineth triangle]
  wait 1000
  play "typekey
  setxy [85 -105] pd setpc "yellow fill pu setxy [135 -45] pd fill pu
  wait 6000
  pr [Here is the tenth triangle]
  wait 1000
  play "typekey
  setxy [85 -45] pd setpc "yellow fill pu setxy [60 -2] pd fill pu
end

---

Procedure	ColorTriangles5
Description	How many triangles do you see of N non-parallel lines?
Level	Intermediate
Tags	Math, Combinatorics